Heaps

A binary min heap is a tree whose children are greater than the parent. This is particularly useful if you want to take the smallest element from a set, etc.

Inserting

Make a node at the bottom, and then iteratively switch it with the parents until order is restored. This is known as bubbling up.

Removing

You can only remove the root. When you do this, replace it with a leaf node. Then bubble this leaf node down until order is restored.

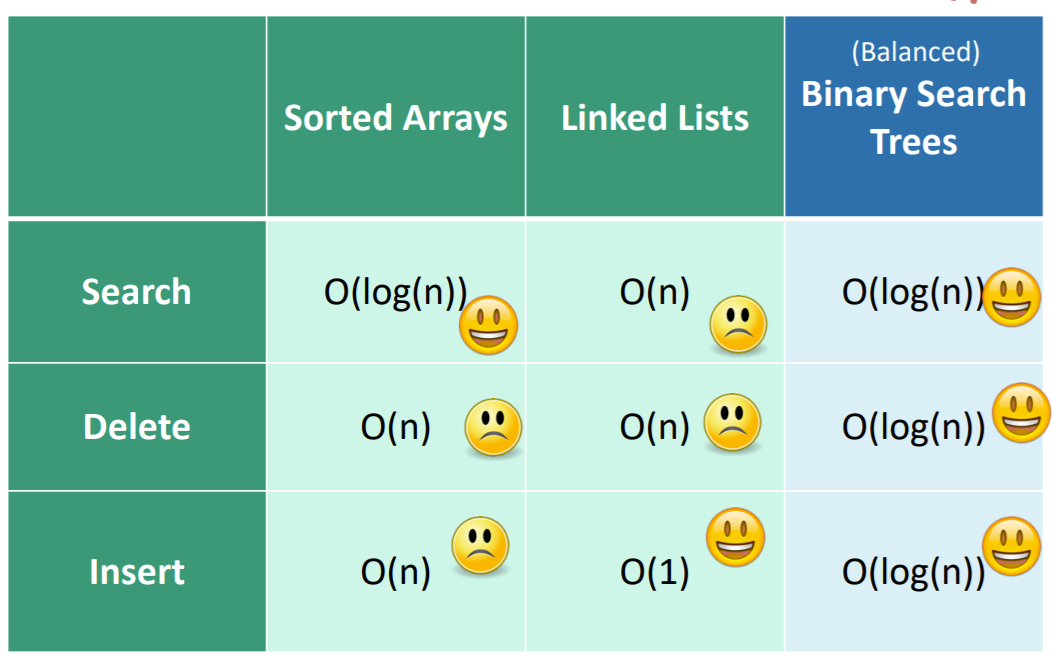
In both cases, the operations are in $\log n$ complexity on average.

Binary Search Tree

A binary search tree has the following properties

1. It has a root node

2. It has a set of child nodes with no children. These have NIL as the children.

3. every element in the subtree to the left of the root node is less than the root node

4. every element in the subtree to the righ of the root node is greater than the root node

Why BST?

It gives us the best even runtime

Making a search tree

This a very simple recursive algorithm that uses a quicksort-ish technique

1. pick a root from the set of numbers

2. partition the numbers into less than and greater than the root

3. Make subtrees using the split sets, join to the root

As a side note, search trees must have unique elements. You can impose an arbitrary ordering if you have identical elements

To output elements in sorted order, just do in-order traversal.

Searching

This is easy! Look at a node. If the element is greater than the node, recursively search the right subtree. Vice versa. When you hit the matching node, return true. If you hit a NIL, return false.

Inserting

Just run the search algorithm until you hit a NIL. This is where the element would have been, so add the element here

Deleting

This one is a bit more tricky. First, find the node. Now, there are three cases

1. node is a leaf: just delete it

2. node has only one child: just delete it

3. node has two children: delete it, but fill with in-order successor.

Why the in-order successor? Well, remember that in-order successor is the element that comes immediately after it in sorted order. The idea is that we still want to maintain the tree property, and this is the closest we can get. The in-order successor is always going to be a leaf node (think about this for a second), so the swap process is painless.

What’s the problem?

Well, so in all three operations there is a search operation. This search operation is the time it takes to traverse the longest path in the tree. In the most balanced tree, this is just $O(\log n)$. However, in the least balanced tree, this can be as bad as $O(n)$.

But how do we enforce the idea of balancing? We could rebalance the tree every time it becomes unbalanced, but this is highly inefficient. Instead, we should make a tree that corrects itself after things become unbalanced enough.

However, this is very vague terminology. Let’s rigorize it in the red-black tree.

Red Black tree

The big idea of the red black tree is that we can measure how unbalanced the tree is, and perform rotations to get it back into shape.

The definition

1. every node is either red or black

2. root is black

3. NIL are black nodes

4. children of red nodes are black nodes (no constraint the other way around)

5. for all nodes $x$, all paths from $x$ to the NILs have the same numbero f black nodes. This is relevant for each node and all possible paths

Intuitively, we should focus on points 4 and 5. Without red nodes, restriction 5 would mean that the tree has to stay perfectly balanced all the time. However, the red nodes add a buffer region. But because red nodes MUST be followed by a black node, we are limited by the amount of buffering we can provide.

In fact, the difference between the shortest path and the longest path in a legal RB tree is just $\log n$ vs $2\log n$. This is best illustrated visually:

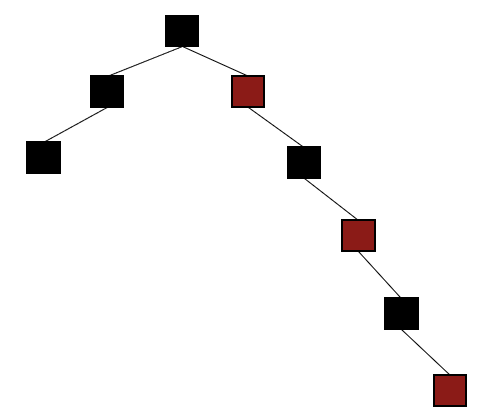
Tricky things

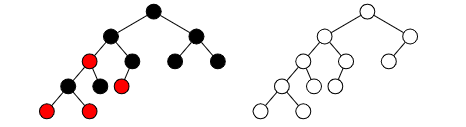
Don’t forget: a parent with one child has the other child as a NIL node. This means that the tree on the right is not a valid RB tree because the right child of the root node, when colored black will have two paths with different number of blacks to NIL

Critical theorems

We want to show that any valid red-black tree on $n$ nodes has height $\leq 2\log_2(n+1)$.

To do this, let $b(x)$ be the black height of some node $x$, which is the number of black nodes from $x$ to NIL, excluding $x$. The number of non-NIL descendants of $x$ (represented as $d(x)$) is at least $2^{b(x)} - 1$. Intuitively, this is true because the blacks themselves, ignoring the reds, will be branching twice per layer which leads to a geometric series that has sum $2^{b(x)} - 1$. but let’s formalize it through induction.

• Inductive hypothesis: for $b(x) = k$ , it is true that $d(x) \geq 2^{b(x)} - 1$ where $d(x)$ is the number of non-NIL descendants

• Base case: $b(x) = 0$ (i.e. this is a leaf node). There is nothing below the leaf and this $2^0 - 1 = 0$, as expected

• Inductive case: Consider the case with $b(x) = k+1$. We note that $d(x) = 1 + d(left(x)) + d(right(x))$. Because $right(x), left(x)$ must is one lower down on the tree, we can use the inductive hypothesis on $d(x)$ to state that

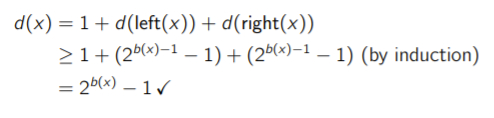
Now, how does this inductive proof help us? Well, we know that $b(x) \geq h(x)/2$, where the $h(x)$ is the height of $x$. This is because we can’t have consecutive red nodes.

Furthemore, we know that $d(x) \geq 2^{b(x)} - 1$, which means that $\log (d(x) + 1) \geq b(x)$

Now, recall that $n$ is the number of nodes in the tree, and $d(x)$ at the root is the number of nodes in the tree. So we finally arrive at

as desired in an RB tree. Phew!!

Maintaining order in RB tree

Now that we have proven that an RB tree satisfies a certain degree of balance when legal, let’s look at how we might make the tree legal.

Philosophically (and we won’t get into extensive detail here), when we add or remove something from an RB tree, we may have to break the RB rules. But...by performing a finite number of actions in $O(1)$ time, we can actually get back a legal RB tree.

Rotations

The rotation is at the heart of how a RB tree works. A rotation will change the root of a tree.

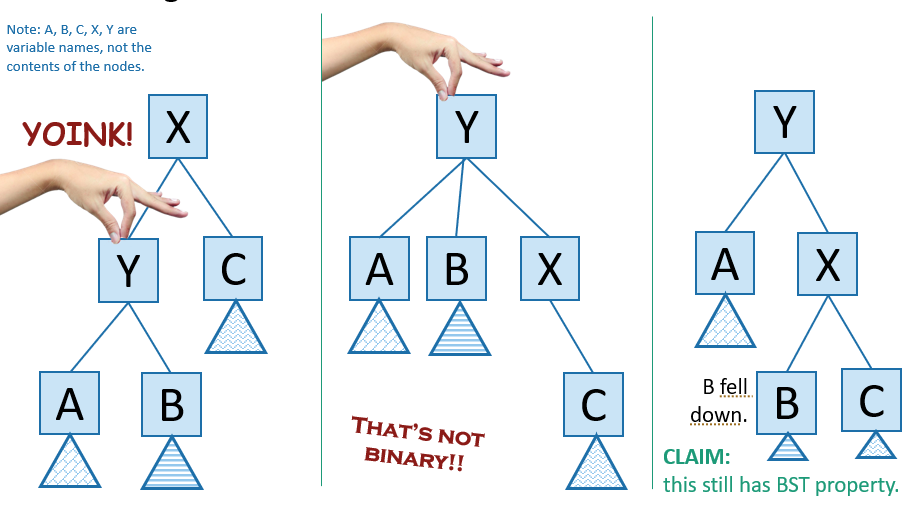
Let’s consider a left rotation

1. Make the parent a child of the target node. This makes an illegal triple child, but note how the parent must be to the right of the existing children because it’s greater

2. Take the middle child of the target node and add it as a child of the former parent. Note that you will always be able to do this because you’ve essentially linearized the original root and this means it’s missing a child (see below)

The best intuitive explanation is if you see the tree as blocks connected with strings. You “grab” a child node of the root and things just pop into place.

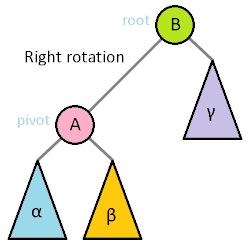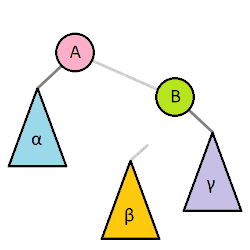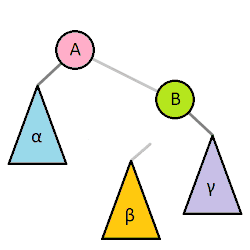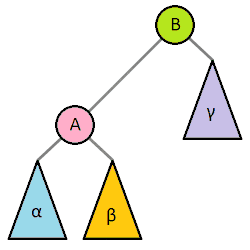
A right rotation is exactly what we saw here except that we go the other way.

We can rotate any subtree in a tree in $O(1)$ time. We just sever the parent of [X], do the rotation, and reconnect the parent to [Y]. This is cool!

Inserting into a RB tree

There are three main cases. Technially nine more cases but let’s just consider three for simplicity

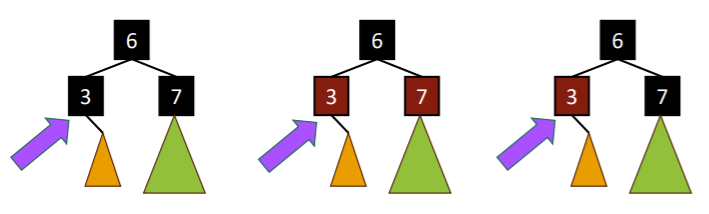
First case

In the first case, just make a red node. This is legal!

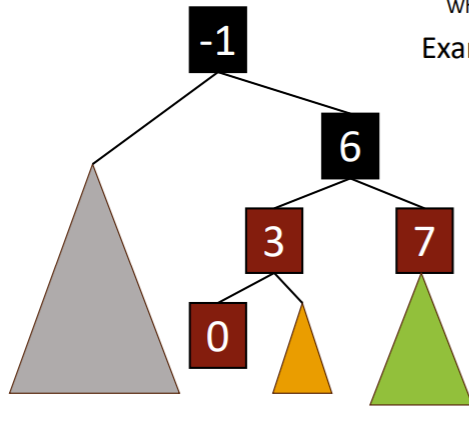
Second case

In these second case, you can’t add another red node. You can’t add a black node either, as it would be unbalanced (adds a shorter path for the blacks)

Here’s what you do:

1. Add as red node

2. flip the parents and grandparents’ colors

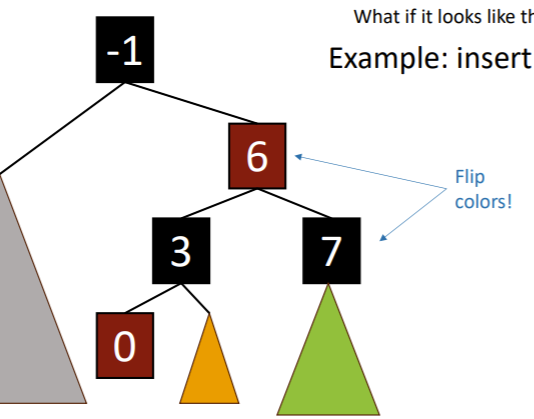
But of course, we might run into a problem if the node above (-1) was red. Well, here’s the deal. At this point node [6] is a balanced RB tree. You want to insert [6] into the rest of the tree, which is the same as inserting any singular element into the tree. It is recursive.

Third case

Well, you make a red node and insert normally. Then, “fix” things up.

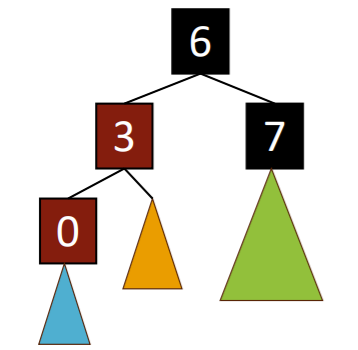
In fact, we are just one rotation away from it working!

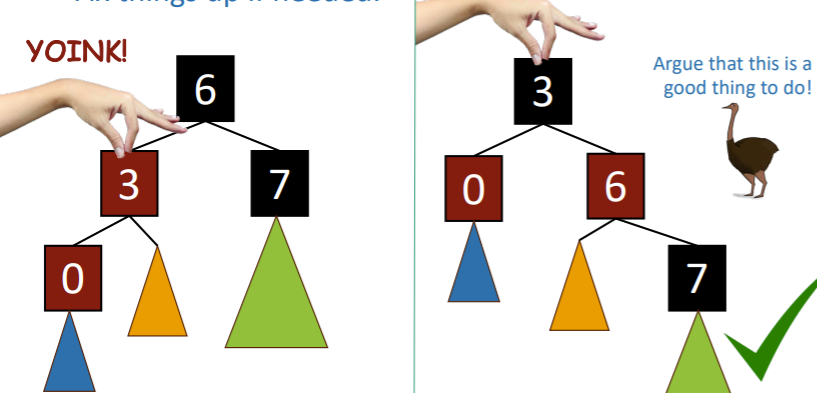
The essence is that we invert the root and node [3] colors.

Challenge question

Say in the worst case, the left of the tree is all black and the right of the tree has maximal red. Let $k$ be the depth of the left half. The right half depth is $2k$. The number of elements in the right half of the tree is $2^{2k}$, and the elements in the left half is $2^k$. The number of elements in the whole tree is $n = O(2^{2k})$. However, there is at least $2^k$ elements to the left of the chosen element and $2^k = \sqrt{2^{2k}}$. Therefore, we say that the chosen element is at most $\sqrt{n}$ from the lowest value. This is a bit tricky!