Insertion Sort

Python code

def InsertionSort(A):
for i in range(1,len(A)):
	current = A[i]
	j = i-1
	while j >= 0 and A[j] > current:
		A[j+1] = A[j]
		j -= 1
	A[j+1] = current

Algorithm

1. start from left to right

2. move current element left until there’s something smaller to the left, or it’s at the beginning

3. keep on doing this

Does it work?

Yes. Proof by induction. Inherently, we build up the sorted list from left to right. We can show by induction that in every step, we contribute to making a larger sorted list until at the end, we end up with only the sorted list.

Inductive hypothesis: After iteration $k$, the array’s first $k + 1$ elements are sorted.

Base case: we start with the leftmost element at iteration zero. One element is always sorted. Inductive case: we start with the first $k + 1$ sorted at iteration $k$. We consider the $k+2$ element. The Insertion sort algorithm will put this element into the appropriate position within the original first $k + 1$ sorted, leading to a list of $k + 2$ elements that are sorted after $k + 1$ iterations, which completes our induction.

As such, after $n - 1$ iterations, the whole list will be sorted.

• Formal proof

  

How fast is it?

Well, in the worst case, every step would require moving the current element to the first element of the array, which is on the order of $n$ steps. We do this for every element of the array, leading to $O(n^2)$ complexity.

Merge Sort

Code

MergeSort(A):
	n = len(A)
	if n <= 1:
		return A
	L = MergeSort( A[:n/2] )
	R = MergeSort( A[n/2:] )
	return Merge(L, R)

Algorithm

1. chop lists into half

2. recursively sort these halves

3. merge them

Does it work?

Yes! Let’s prove this inductively.

Inductive hypothesis (strong induction): when returning an array smaller than $k$, this array is sorted.

Base case: one element is always sorted

Inductive case: suppose we get an array of size $k + 1$. We split it up and ask merge sort to sort $(k + 1) / 2$ arrays, and by our strong inductive hypothesis, these are sorted. The merge operation will then ensure that these two sorted arrays will produce one large sorted array. And as such, we complete our induction.

• Proof that merge works

  This is another proof by induction. Hypothesis: a list of size $k$ and any other size list will be merged properly. Base case: if $k = 0$, then that list is already merged. Inductive case: start with $k + 1$, and then show that you can start the merging process and eventually you’ll end up by taking one element from this $k + 1$ list. At this point, induction takes over. (this is very informal)

• Formal proof

  

How fast is it?

Well, when dealing with a recursive algorithm (more on this later), we focus on the recursive step, and the the processing step. So, the time taken is equivalent to the time sorting two lists of n/2 size, along with the final merging.

However, we understand that the recursive sorting involves more merging. So why don’t we just expand this tree out and focus on the merging?

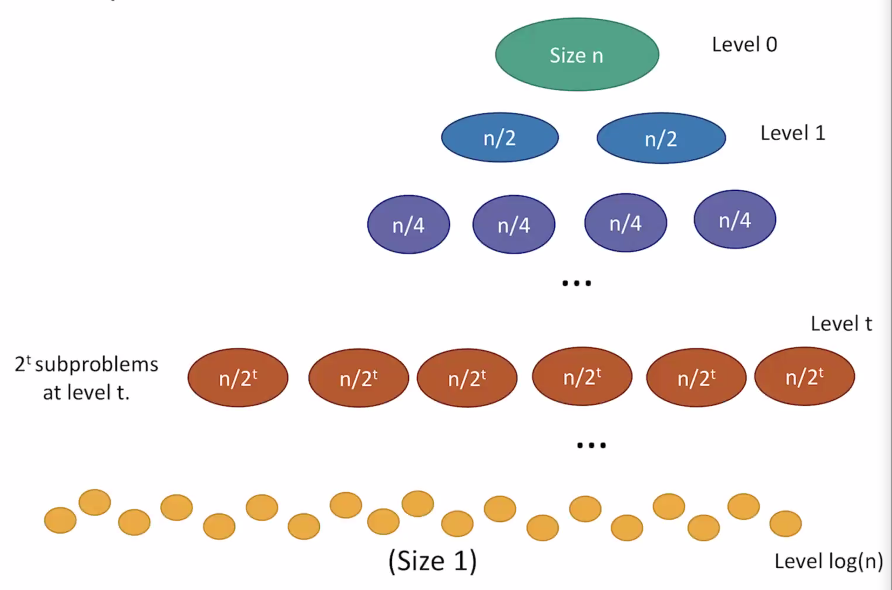
On every level of recursion, there are $n$ elements to be merged. There are $\log_2(n)$ levels, which means that the total amount of time is $n \log_2(n)$. This accounts for a complexity of $O(n\log n)$