Randomized Algorithm Analysis

Tags	CS161Complexity

Measuring randomized algorithms

There are two ways of quantifying randomized algorithm. First, you can look at the expected runtime. This is when you have an adversarial input but a random sampling process. The adversarial input is key! The adversary chooses BEFORE you take the expectation

You can also look at worst-case runtime, which is when you have an adversary pick the input as well as the random chance outcomes.

The formalism

We want to find $E[T(n)]$ . This not the same as $T(E[n])$ because the $T$ is not a linear function.

Quicksort

Implementation

pick a pivot

partition array into elements less than and greater than the pivot

recursively call quicksort on these smaller segments

weld the outputs together

In-place implementation

It’s often more efficient to sort arrays in place. You can achieve this by using two sticks

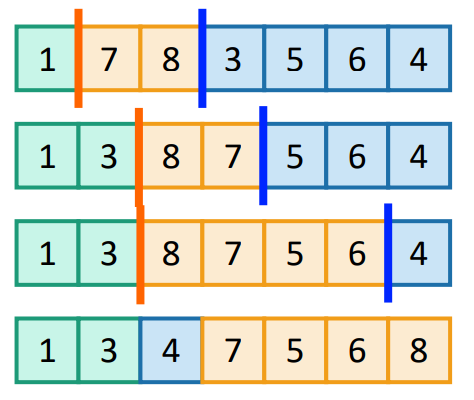
pick pivot, move it to the end

start with blue and orange sticks at the beginning

Move blue stick and compare element on its right to the pivot
1. if an element is less than the pivot to its immediate right
1. swap with the position immediately to the right of the orange stick
1. advance blue stick by one, orange stick by one.

Worst case complexity

Our recurrence relationship is

T(n) = 2T(|L|) + T(|R|) + O(n)

Now, this $|L|$ and $|R|$ are random variables. But in the worst case, we can assign the pivot as the least or the greatest element. This pushes everything into one partition, which yields

T(n) = T(n-1) + O(n) = O(n^2)

Analysis of complexity: what doesn’t work

We might think to ourselves, hmm $E[|L| + |R|] = (n-1)$ , so it must be the case that

E[|L|] = E[|R|] = (n-1)/2

and so you can plug it into the recurrence relationship

T(n) = 2T((n-1)/2) + O(n)

and by the master theorem you get $T(n) = O(n \log n)$ . Right? WRONG!!

☝

This demonstrates an important fallacy. Above, we computed

T(E[n])

whereas we really needed to compute

E[T(n)]

Analysis of expected runtime: what does work

Instead, let’s think about what actually contributes to the runtime. It’s these comparisons that we make during the partition. If we can find the number of comparisons as a function of $n$ , this is our complexity!

More specifically, let $X_{ab}$ be the indicator variable between two numbers in the list. So if $X = 1$ , then a comparison has happened. We want to find

E\left[\sum_{a = 1}^{n-1}\sum_{b = a + 1}^n X_{a, b}\right]

Now, let’s consider an array of size $n$ whose elements are just the numbers from 1 to n, for simplicity. We can use element notation, but it’s easier to wrap our heads around a real example.

Consider two numbers $a, b$ . When will they never be compared? Well, if the pivot is chosen between $a → b$ , we separate them forever. If the pivot is chosen as one of $a, b$ , then we are guaranteed to compare them! And if the pivot is chosen outside the range $a→ b$ , we can’t say the chance at the moment (hmm why can we assume this?)

Therefore,

P(X_{a, b} = 1) = \frac{2}{b - a + 1}

The 2 comes from the ability to choose the pair, and the $b- a+ 1$ is the elements in-between the two, including the two selected.

Think for a second why this is the case. And now, the expected number of comparisons is just

\sum_{a = 1}^{n-1}\sum_{b = a + 1}^n E\left[X_{a, b}\right] = \sum_{a = 1}^{n-1}\sum_{b = a + 1}^n\frac{2}{a - b + 1}

We can take the inner sum first and we arrive at this inequality (factoring the 2 out first)

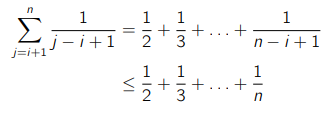
We note that this is a harmonic series, and we have the following deriveation

Derivation

So $\sum_{k=1}^n \frac{1}{k} \leq \ln n$ , which means that the following is true (we use different variables than $a, b$ in these examples but they are the same mathematically)

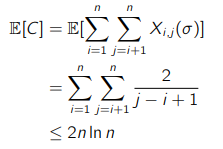
This means that the expected runtime is $O(n\log n)$

Merge sort vs Quick Sort

Quicksort has a bad worst-case outcome of $O(n^2)$ but the expected outcome is $O(n\log n)$ . Mergesort on the other hand always has $O(n\log n)$ complexity.

We can do quicksort in-place, while merge sort in-place is not trivial, especially if you want to keep sort stability (elements with same key do not get moved around)