Introduction

• degree and neighbors represent connections of a vertex

• In directed graphs, we refer to in-degree and out-degree when talking about number of connections. Similarly, we refer to incoming neighbors and outgoing neighbors

Representing graphs

We can use an adjacency matrix $A$ such that $A_{ij}$ are the nodes that go from $i$ to $j$. In an undirected graph, the adjacency matrix is symmetrical.

We can also use an adjacency list such that each index is a node and each element is a linked list corresponding to the nodes it is connected to

Questions we can ask

• Edge membership: is an edge $e$ in the graph?

• Neighbor query: what are the neighbors of vertex $v$?

Matrix vs list

In edge membership, it takes $O(1)$ time to find if an edge $\{v, w\}$ is in $E$. On the other hand, it takes $O(deg(v))$ or $O(deg(w))$ to find it in a list. This is because you need to search down the linked list at the desired node.

For neighbor query, it takes $O(n)$ time in the matrix to extract a row and read it, while in the list, it takes $O(deg(v))$ to read and extract the linked list.

In terms of space requirements, the adjacency matrix takes $O(n^2)$ room. What about the list? Well, for every edge, there are two entries in the list. Furthermore, there will be $|V|$ entries in the table. Therefore, there will be $2|E| + |V|$ entries, with complexity $O(|E| + |V|)$.

In general, the list representation is better for sparse graphs

Depth-first search

For each node, you keep track of a state. This state can be new, explored, or depleted. Technically you only need two states but for comprehension purposes it’s easier to have these three. Here’s the DFS algorithms

1. Start at some node, mark it as explored.

2. Pick a new node that is a neighbor of this node, run DFS on that (recursively). Keep on trying this.

3. Once you get to point where there are no new nodes that are neighbors, you mark the current node as depleted and return

The intuition

There are a few ways of understanding DFS. First, you can see it as exploring a maze with a piece of chalk and a ball of yarn. You go as deep as possible, and you only go back once you’ve exhausted every possible option at this location.

You can also understand this as making a tree graph as deep as possible.

Visually, it also looks like shooting down first, and then gradually making your way up, and then shooting down again, etc.

DFS makes trees

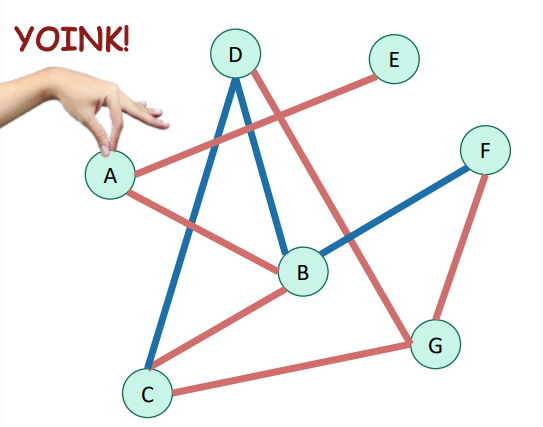
If you marked all the edges you search, you would make a tree. You don’t indulge in cycles because you only explore a node once. That’s the magic of it. And again, trees are trees regardless of the root node, but in this case, it makes sense to define the tree WRT the starting node. In this case, you will see that the tree is as deep as possible.

If you look at the other side of the story, if you ran DFS on a tree itself, it would return an in-order traversal of the branches.

DFs finds connected components

Because DFS makes a minimally-connected component graph, it is a great way of finding connected components in a graph.

Runtime analysis

Intuitively, to explore the connected component, we look at each edge at most twice, once from each of its endpoints. We don’t worry about travel time, etc.

More rigorously, at each vertex $v$, we consider everything in its neighbors leading to $O(deg(v))$. Summing this up will lead to $2|E|$ from a graph theoretical standpoint. Therefore, the final complexity is

And in a connected graph, it must be the case that $|V| \leq |E| +1$ from graph theory. Therefore, our final complexity can be simplified down to

Now, this was just to search the current connected components. What about the whole graph? Well, in this case, the inequality $|V| \leq |E| + 1$ doesn’t hold, and you must consider the whole thing, $O(|E| + |V|)$

DFS on directed graphs

The DFS algorithm works on directed graphs and returns a minimal spanning tree!

Topological sort and “timing”

Let’s keep track of the “in time” and “out time” of each node. Let’s say we have a wall clock, and every time we make a step, the clock ticks. We can mark the time we first hit a node to the time we mark the node as depleted. This “finish time” can be important in making certain algorithms.

What this looks like

Go depth first. Every time you hit a node, you increment the timer. The first node you hit is time $0$. When you backtrack and pick another node, you shouldn’t count the backtracking as one step. Essentially, you only tick the time if you find a new node or you close out an old node. This also means that when you reach a terminal node, the clock ticks twice. Once for entry and once for closing.

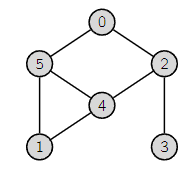
For example, node $2$ has entry time of 1, and an exit time of $10$.

On a directed graph

If you’re doing this on a directed graph, it’s not any different! Do NOT restart the timing in-between. Pick up where you left off after you finished one connected component.

DAG

First, let’s talk about the setup. In a dependency graph, the structure is a Directed Acyclic Graph, meaning that the edges have directions (dependencies) and that there are no cycles, meaning that you can’t have a triangle of things depending on each other.

A tree is a DAG but a DAG is not a tree. To be more specific, because the graph is directed, it may be the case that there are loops but the directions are such that there isn’t a cycle. More formally, a DAG node can have multiple parents while a tree can only have one parent. s

We want to sort the nodes in such a way that we know what is the node that everything depends on, and so on. If we are talking about package dependencies, this is the package that you would install first.

Finish times are useful

Claim: if $A$ is the parent or ancestor of $B$, then $B$ must “finish” before $A$ in the DFS. Think about this for a quick second and see if that makes sense. When you pass $A$ on the way to $B$, you “open” up $A$ but you don’t “close” $A$ until you close $B$ as you make your way back up.

BFS (Breadth first search)

if DFS was like exploring a labyrinth with a spool of yarn, BFS is like flying over a city!

You start at a start location, then you explore everything you can reach in one step, then explore everything you can reach in two steps, etc

Intuition

So the BFS is also building a tree but this time, the tree is as wide as possible

More importantly, each layer of the tree represents a ‘ring’ of neighbors. So the root is zero steps from the root, the first children are one step from the root, etc.

Shortest path

To find the shortest path between $w, v$ you just run BFS from $w$ or $v$. This works because you want to minimize the distance to any node (which isn’t the case for DFS)

To find the distance between $w$ and all other vertices $w$, just make a BFS tree starting at $w$, and then the shortest path between $w, v$ is just given by the BFS tree

Compare and contrast

Both searches create a minimally spanning tree, but DFS makes the deepest possible tree while BFS makes the widest possible tree. In terms of functionality, it’s the same thing except we use stacks vs queues. The stack immediately goes deep, while the queue will push further exploration to later.

Bipartite graphs

Given a graph, can we separate into two components that aren’t connected into each other?

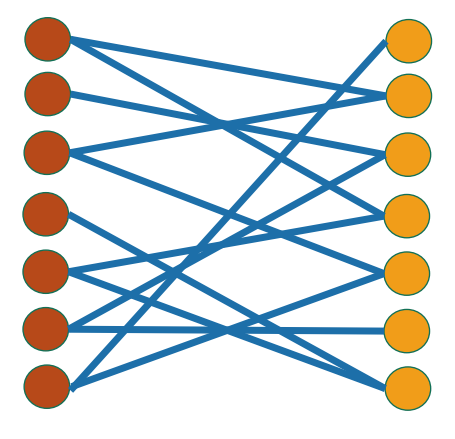
Testing bipartiteness

Bipartite graphs means that as you start traversing, each step moves you to the other side. If you do a BFS, this means that each layer of the tree should be different “sides.”

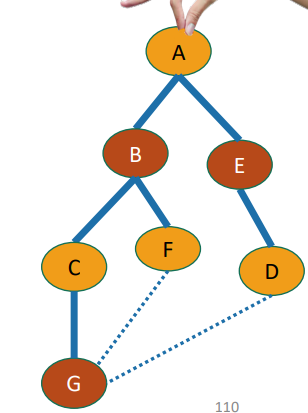
So, to test bipartiteness, you color the BFS tree in alternating colors, and then you look at the additional edges that we didn’t include. If the edges connect like-color to like-color, then it means that we can’t separate out the graph into a bipartite setting.

Proof

Elements of the same color in a BFS tree are the same distance from the root, or have distances an even number of traversals apart. This is also the case with a bipartite graph. Same color nodes have this very property.

So, if the BFS tree nodes of the same color are neighbors in the actual graph, it means that the two nodes are part of an odd length cycle. Take a moment to think about this. We have two same-parity appendages and we join them with one extra edge, it must be an odd cycle.

However, in an odd cycle, you can never color the nodes such that no two neighbors have the same color. This is more of a “duh” statement but it might take some time to understand why.

As such, if elements in the BFS tree with the same color are neighbors, then the whole graph is not bipartite