Recipe

1. optimal substructure (hardest)

2. recursive formulation

3. dynamic programming

4. bookkeeping (for reconstruction’s sake)

Tips

• Start with a solved largest problem. What can you guarantee about a smaller problem? (think: subpaths of an optimal path)

• Look at the full problem and think about how you can boot the computation to a smaller problem by splitting it into cases

• Start with a solved smaller problem. How can you make it larger.

• look for “paths” that allow you to express something complicated through iterations of recursion.

Longest Common Subsequence

Simple task: given two strings $X, Y$ of length $n, m$, find the longest subsequence that they share in common. A subsequence is formed when you remove characters from a string

Optimal substructure

Here, we rely on one key insight. Look at the last character of both strings.

1. If they are the same, then this last character is necessairly part of the longest common subsequence

2. If they are different, then at least one of the last characters is not part of the longest common subsequence, so you can essentially chop off the last character. But which one? Well, that you don’t know. You must find out by trying both!

Recursive formulation

Let’s use a table to keep track of our results. In top-down recursion, the table would just be a recursive call. However, today we are focusing on bottom-up solution approaches. As such, we define $C[i, j]$ to be the longest common subsequence with strings $X_i, Y_j$ where $X_i$ is the prefix of $X$ with the first $i$ characters, and same deal with $Y_j$.

If $X[i] = Y[j]$, then

What about if $X[i] \neq Y[j]$? Well, you’ve got some exploring to do!

The two components essentially try the strings with one character removed. Implicitly, it also tries the the strings with both end characters removed, in the next step (just roll out what $C[i-1, j]$ is equal to)

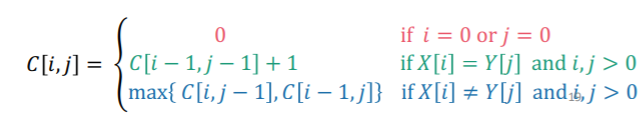
Dynamic programming

You start with the base case, and then you build up the table row by row. At element $C[i, j]$, you apply the recursive rules that we defined above. This either means adding one to the diagonal, or picking the maximum from the left and the above cells. This would be a bottom-up programing algoriithm

For a top-down programming algorithm, you would make a recursive call every time you wanted to find the $C$ of a smaller problem, but you would keep track of a table and short-circuit the recursion if you find that it has already been solved.

Bookkeeping

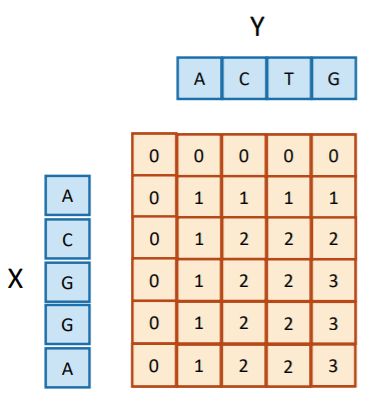
Now, how do we reconstruct the LCS from the table? You can use the naive approach, which is to keep track of your string as you go. However, this does have a high space complexity.

To mitigate this, you can use a clever backtracking strategy. The lower right corner of the table is the answer you get when you call $i = n, j = m$ (i.e. with the whole string). Now, you apply the following algorithm on the table

1. Look at $X[i], Y[j]$. If they match, pick this character and move diagonally.

2. If they don’t match, find the element that was copied to the current element. This is either above or to the left. Go there, but don’t pick any characters. If there are ties, your choice doesn’t matter.

When you reach any $0$, you have reconstructed the LCS (albeit backwards).

Complexity analysis

To fill the table, we need $O(nm)$ steps. If you are not concerned with the final answer, we can actually skip the table and just keep the last two rows in each iteration of the algorithm, because the decomposition never goes before $i-1$ or $j-1$.

Challenge problem

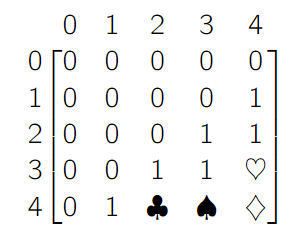
$X$ is the rows and $Y$ are the columns. What can you say about $X_2$ vs $Y_4$? Well, you can use the following chain of logic

1. We know that $X_2 = Y_3$ because that’s a one surrounded by zeros

2. We know that $X_1 = Y_4$ because of similar reasoning

3. However, we know that $X_1 \neq Y_3$ because it’s a zero. Therefore, there is no equality ‘bridge’ between $X_2$ and $Y_4$, meaning that $X_2 \neq Y_4$.

You can do the same reasoning pattern for the symbols to figure out the rest of the matrix.

Knapsack problem: unbounded knapsack

Given items with $i, ..., k$ with weights $w_i$ and values $v_i$, what’s the most value I can get with a capacity of $n$? Let’s start with a simple iteration of the problem, which assumes that you are in a warehouse and can take as many things of item $i$ as possible.

Subproblem decomposition

If you have an optimal knapsack and you take away an element, this smaller knapsack must also be optimal for that size. This is because if it wasn’t optimal, then you can add that element back into the true optimal smaller backpack and create an even more optimal original knapsack, which is a contradiction.

Therefore, if you have a capacity $W$, the optimal packing is the best you can make $W-w_i$, plus a new object $V + v_i$. You have multiple objects, so you must try them all.

Recursive Formulation

So, if you define an array $K$ such that $K[w]$ is the best possible value for a specific weight $w$, you can define the relationship as

If there is no such $w_i$ such that $w - w_i > 0$, then $K[w] = 0$.

Dynamic programming

You can just use this recurrence relationship to build a bottom-up algorithm

Challenge problem

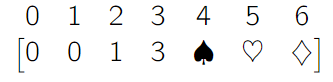
What can we say about this?

1. Because $2$ is the first knapsack that has non-zero value, we conclude that there is one object of weight 2 and value 1

2. Because there are no objects of weight 1, we conclude that there must be one object of weight 3 and value 3

3. Therefore, the minimum value of the knapsack at weight limit $4$ is just $3$, because you can just use the knapsack of weight $3$. It’s a minimum because we don’t know if there is a weight 4 object.

4. We can also say that the minimum value of the knapsack with limit $5$ is 4, becuase we can add the objects of weight 2 and weight 3 together .

5. We can also say that the minimum value of the knapsack with limit 6 is 6 because you can add two objects of weight 3 together.

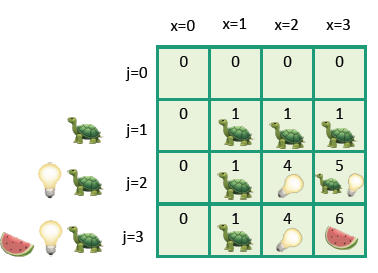
Knapsack Problem: 0/1 Knapsack

Here, we have a small problem. Previously, we were able to do $\max_i$ and find the best thing to add. However, if we can only take one of each item, we can’t blindly optimize. We must formulate a different solution.

The insight

If we are given the use of the first $k$ items, we can either choose or not choose to use the $kth$ item. If we don’t choose the $kth$ item, then we default to the optimal bag that has the same capacity but operating on the first $k-1$ item. If you choose the $kth$ item, then you reduce the capacity and you look at the optimal bag with reduced capacity on $k-1$ item.

This sounds like a job for...2D array!!

The setup

let $K[w][k]$ be the optimal value at capacity $w$ with the first $k$ items available.

The code

and this is what it looks like in tabular form

Independent Set

An independent set in a graph is a set of vertices such that no pair has an edge between them. We want to find the independent set with the largest weight. The original question with the random graph is actually NP complete. So that’s no good. Let’s try a tree!

Hmmm. Let’s use the strategies that we’ve learned so far and see where they can take us. Let’s try building things up. A tree can be split into subtrees. In each subtree:

1. the root can be selected. Then, its children can’t be, but the children of those children are just more subtrees

2. The root may not be selected. Then, its children are subtree problems.

The approach

Keep two arrays. Let $A[u]$ be the weight of a maximally independent set rooted at node $u$, and let $B[u]$ be the sum of weights of the children at $u$, assuming that $u$ is not selected. Technically, this distinction is not necessary but it helps for notation. As such, you have

Note how the first term is when the root is not selected, and the second terms is when the root is selected.

Dynamic programming

Here, we actually use a sort of bottom-up approach, even though we use recursion to get to the leaf nodes. This is because we need the children (base case) to be filled before we make our way up. It’s still bottom up.

This is different from recursive divide and conquer because you are taking advantage of overlapping subproblems!

Because you only fill up each entry once, the complexity is $O(|V|)$. Nice!

Binary numbers

What is the number of binary strings of length $k$ you can make such that there are no repeated $0$’s?

• Key insight: no matter what, we can take the previous string and add one.

• Second key insigth: no matter what, we can take two strings before and add $10$.

• Third key insight: we can’t add $11$, because that’s covered in the first insight. We also can’t add $01$ because that might be illegal

So, you make $A[i]$ where $i$ is the length of the binary string. We have

with a base case of $A[1] = 1$ and $A[0] = 0$.

More examples

• Store a table where $A[i]$ is the maximum product you can make with length $i$. Then, compute the max of $c A[k - c]$, where $c \in [2, ... k]$. Build bottom-up

• recursive insight is that on a 2d grid, we look at all the places where in one hop, a knight can end up at the target location. Add those up.

• To do this, start with an $8\times 8$ array of zeros, and for each element, look at the knight-neighbors (locations that are reachable by one knight hop). Then, add them up and do this for all of the elements. At the end, you just need to return $A[k][x][y]$.