Dynamic programming

Dynamic programming is the simple idea that you use subproblem answers to build up to the real answer.

Fibonacci example

The traditional fibonacci recursive algorithm runs in $\Omega(2^{n/2})$ time, which is not good.

But look at this:

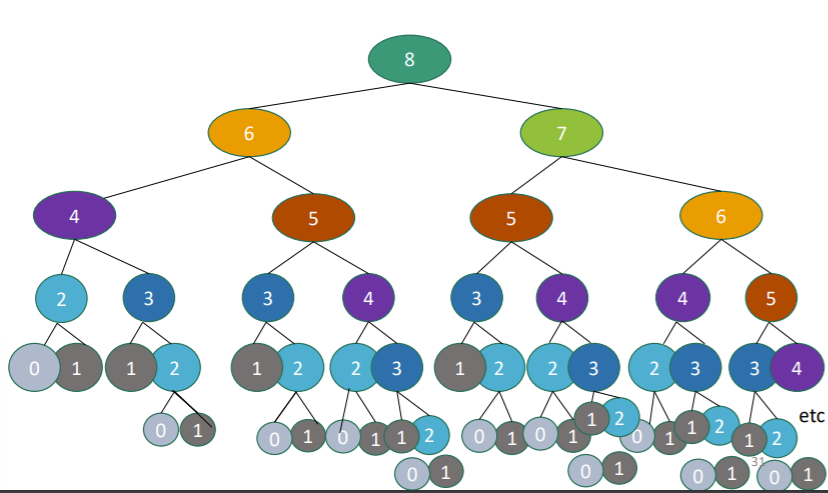
There are so many repeated computations!

Memoization

To help, why don’t we make an array that stores past computations and short-circuits recursion when needed? This is known as memoization, and it is a form of top-down dynamic programming. More on this in a hot sec.

Using the recurrence

Why don’t we build up the fibonacci sequence from the beginning? This means starting with $F_1 = 1, F_2 = 1$ anmd then bullding $F_k$ using the recurrence relationship. This is known as bottom-up dynamic programming. More on this later.

In both cases, we turned the computation from exponential to linear.

Building Dynamic Programming Algs

What is necessary?

• Substructure: you can divide the problem into smaller problems

• Repeatable substructures: each divide-and-conquer step is repeated many times. In the fibonacci example, we note how we can reuse past answers easily. In Bellman-Ford, we are able to use the same array for each vertex.

Bottom-up

1. solve the smaller problems first

2. build up the problems until you have the solution to the bigger problem

Top down

This is the traditional recursive algorithm. Solve the bigger problem by solving a smaller problem, etc. But keep tabs on problems that have already been solved. It’s like you’re trying to build a house but you know that society has already solved power tools and so you don’t need to build them yourself.

Both approaches have the same complexity but the difficulty of implementation can be different.