Sorting paradigms

When we think of sorting, we must ask ourselves, “what is the input, output, and the operations allowed?” Depending on these answers, we might different limits on how fast we can go.

Bucket sorting

‘But it is true that we can get a better complexity if we change the assumptions up a bit. Now, what if we are dealing with “nice” integer numbers from $1, ... k$?

Counting sort

1. Make an array of size $k$

2. Go through the list and tally up the presence of each number in the appropriate array index

3. At the end, read off the array of size $k$ and for each element $k[i]$, output $i$ with a repetition of $k[i]$.

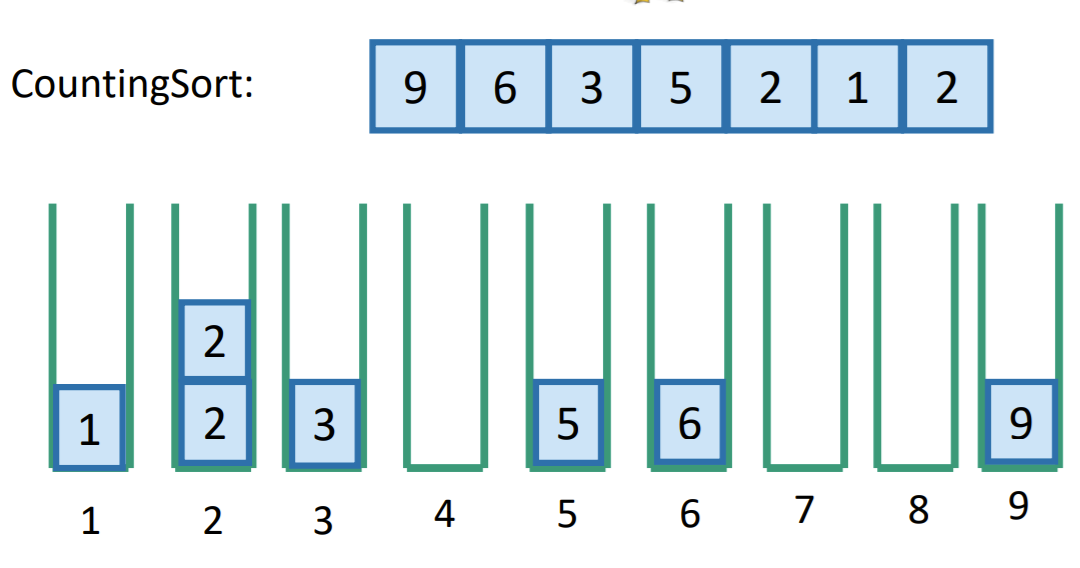
This is a really micro brain sort but it actually works in $O(n)$ time! However, there is a pretty big downside. If $k$ is very large, you will have problems. And it is typical that $k$ is larger than the list size $n$, lest you repeat values.

Radix sort

This is a modification to counting sort that actually works decently.

1. Run bucket sort using the least significant digit

2. recombine into a new list

3. repeat step 1 but you use the second least significant, third least significant, etc. When you get to the end, the recombined list is the sorted list
   1. if you encounter the end of some number (i.e. you are sorting 100, 2, and 45), just pad with zeros

Radix sort proof that it works

Here’s a proof by induction on a list with values $x = [x_{i-1}, ... x_1]$ where each $x_k$ is a digit. Our inductive hypothesis is that at step $k-1$, the elements $x_1, ... x_{k-1}$ are in sorted order, hierarchically. This means that if $x_{k-1} < y_{k-1}$, then it $x$ comes before $y$. If these elements are equal, then we break the tie by looking at $x_{k-2}$, $x_{k-3}$, and so on. Intuitively, this ordering comes about from the stable concatenation operation and the reverse significance sorting order.

• Base case: there is nothing done, so our inductive hypothesis is vacuously true

• Inductive case: after sorting by $x_k$, the first part of the hypothesis comes true automatically, in which if $x_k < y_k$, then $x$ comes before $y$ in this next list. If $x_k = y_k$, then the previous ordering is kept, in which if $x_{k-1} < y_{k-1}$, it is true that $x$ comes before $y$. Again, we keep the previous ordering because we move through the list from left to right, so if two things sorted at $x_k$ go into the same bin, the one that got read first will be placed into the bin first. Therefore, our induction is complete!

Radix sort complexity analysis

So let’s start simple. If you have $d$ digit numbers, the complexity is $O(dn)$, or $O(n)$. Hey, this is cool. But wait...

If in the list of size $n$ you will have numbers from $1→ n$, then $d \approx \log n$. And suddenly our complexity becomes $O(n\log n)$. Ooops...

But wait! We can change the base! We calculate $d$ by doing $d = floor(\log_r n) + 1$, where $r$ is the base that we bucket in. The larger the $r$, the more buckets but the fewer digits to sort. For some intuition about the definition of $d$, think of $r = 10$ and $n = 9$. The log is below 1, but we do have one digit. Therefore, we take the floor and add 1.

Let’s put this together. Let $M$ be the maximum number, and $r$ be the base. In each sort, you need to look across $n$ numbers and initialize $r$ bins. This yields

How do we choose $r$? Well, we can let $n = r$, and now we get

We pick $n = r$ because we want as large of an $r$ as possible, but if we make $r$ any larger than a scalar multiple of $n$, then it will contribute a polynomial factor to the sort, which is not good.

If $M \leq n^c$ for some finite constant $c$, then we have $O(n)$ complexity. However, if $M = 2^n$, then we have $O(n^2 / \log n)$, which is pretty bad.

(as a sidenote, we don’t drop the $+1$ because it still is related to $n$ when you distribute, and $r$ in the original expression. It’s important to be careful of these things!)

Challenge questions involving lower bounds

If this algorithm existed, then you can do a divide and conquer sort such that

If we just roll this out, we can kinda see that we add $O(n)$ for $k$ times, where $k$ is the number of times you need to apply a logarithm until you reach $1$. This we know as $\log^*n$. However, it means that we can sort in $O(n\log^*n)$ time, which is impossible using comparison-based sorting.

Why is this impossible? Well, if we can do all three things, we can just add an unsorted list in $O(n)$ time, and then pluck out the smallest objects in $O(n)$ time, yielding an $O(n)$ complexity sort that would violate our previous proof of the lower bound of $O(n\log n)$.